Circle Packing Revisited

May 01, 2009 | 1 Minute Read

When I originally set out to determine how many optical fibers would be supported by each Ifos lens, I discovered the answer was related to the ongoing research problem of Circle Packing.

Luckily, I found an online calculator to compute the theoretical maximum, and the numbers looked reasonable. There was a problem, however. I found other sources that didn’t agree with the numbers generated by the calculator.

Since I haven’t run across anything to explain or support the calculator’s underlying formula, I’m inclined to prefer Eckard Specht’s simple table, especially since his excellent visualizations make them observable and verifiable.

Eckard’s data show that the ratio $R / r$ is a very smooth function of $N$, where $N$ is the number of congruent circles of radius $r$ that can be packed into a circle of radius $R$.

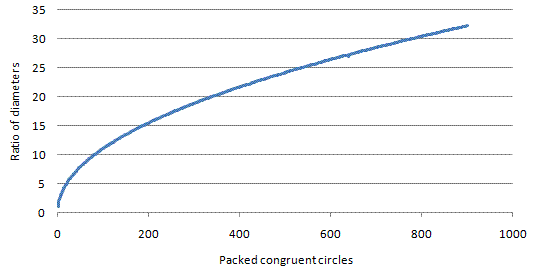
The close correlation is dramatically highlighted by plotting both axes on logarithmic scales. The least-squares approximation is a power function of the form $y = ax^b$.

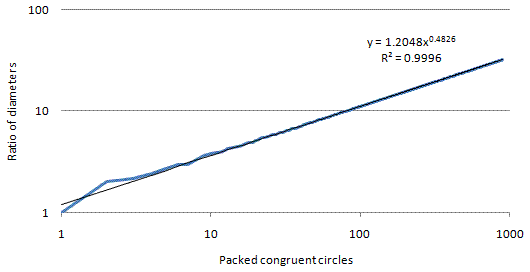
From this, it’s easy to derive an expression to approximate $N$ for any $R$ and $r$:

$$\begin{align} \frac{R}{r} &= aN^b\\ \frac{R}{ar} &= N^b\\ \left(\frac{R}{ar}\right)^\frac{1}{b} &= (N^b)^\frac{1}{b}\\ N &= \left(\frac{R}{ar}\right)^\frac{1}{b} \end{align}$$

The values of $a$ and $b$ from the chart above are generally good, but Eckard has computed better ones for different intervals of $N$. From his site, I let $a=1.203885$ and $b=0.482409$ for $21 \leq N \leq 500$. It’s straightforward to create a simple calculator (below) based on this formula, from which I obtain a different answer to my original question: 81 fibers is the theoretical maximum for a lens 5 mm across, assuming each fiber is 0.5mm.